| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 회귀분석
- 다항로지스틱회귀분석
- people analytics
- Talent Analytics
- PeopleAnalytics
- Text mining
- Pa
- DataDrivenHR
- HR 데이터 분석
- 피플애널리틱스
- HRCommunity
- survival analytics
- 태그도 많이 치는거 힘들다..
- 피플 애널리틱스
- HR 애널리틱스
- HR데이터
- hr스터디
- PA 미래
- 하나만 쓰자..
- 데이터분석
- HR Analytics
- hr애널리틱스
- Workforce Analytics
- ChatGPT
- HR
- HRProfessionalNetwork
- PA201
- HRAnalytics
- HR대시보드
- HRA
- Today
- Total
PA201: People Analytics 201
People Analytics를 위한 기초 회귀분석 본문
1. 개요
PA201 3기에서는 Handbook of Regression Modeling in People Analytics 책을 바탕으로 각 스터디 그룹이 큰 줄기의 통계학 이론과 더불어 가상의 사례를 활용하여 R 활용법을 다룰 예정입니다. 첫 번째 챕터에서는 선형 회귀에 대해 알아보려고 합니다. 선형 회귀는 기본적인 학습 방법 중 하나로, 간단한 구조에도 불구하고 다양한 상황에서 매우 유용한 도구로 활용됩니다. 따라서 선형 회귀의 개념과 어떻게 활용되는지 예제 데이터 셋 with R을 통해 실제로 알아보겠습니다.
2. 회귀분석의 목적 및 개념
회귀분석은 데이터 간의 인과 관계를 정밀하게 분석하고 이해하는 데 주로 사용됩니다. HR 분야에서는 회귀분석을 활용하여 직원의 성과나 퇴직과 같은 현상을 예측하고 이해하는 데 중요한 역할을 합니다. 이러한 분석을 통해 어떤 요인들이 성과에 영향을 미치는지, 또는 직원의 퇴직에 어떤 조건들이 기여하는지를 정량적으로 분석할 수 있습니다.

여기서, 회귀분석의 중요한 부분은 상관관계와 인과관계를 구분하는 것입니다. 두 변수가 함께 움직인다는 상관관계는 인과관계를 의미하지 않습니다. 예를 들어, 더운 날씨에 아이스크림 판매가 증가하고 화상 사고가 많아지는 현상 사이에는 상관관계는 있지만, 아이스크림 판매가 사고를 직접적으로 유발한다고 볼 수는 없습니다. 회귀분석은 이러한 상관관계를 넘어서서, 한 변수가 다른 변수에 미치는 실제 영향을 수치로 나타내어, 복잡한 데이터 속 인과관계를 드러내줍니다.
선형 회귀분석은 이 과정에서 기본적인 툴로 사용되며, 각 변수의 영향력을 선형적으로 모델링하여 변화가 다른 변수에 미치는 평균적인 영향을 추정합니다. 이를 통해 데이터를 바탕으로 한 insight를 얻을 수 있고, 실제 의사결정에 있어서 신뢰성 있는 정보를 제공합니다.
1) Variables & Linear in parameters
- 변수 : 관측하여 자료를 얻게 될 어떠한 것 (ex. 임금, 교육수준 등)
- 선형 모델 : 두 변수에 선형관계(직선형, 1차 함수)를 설정한 모델
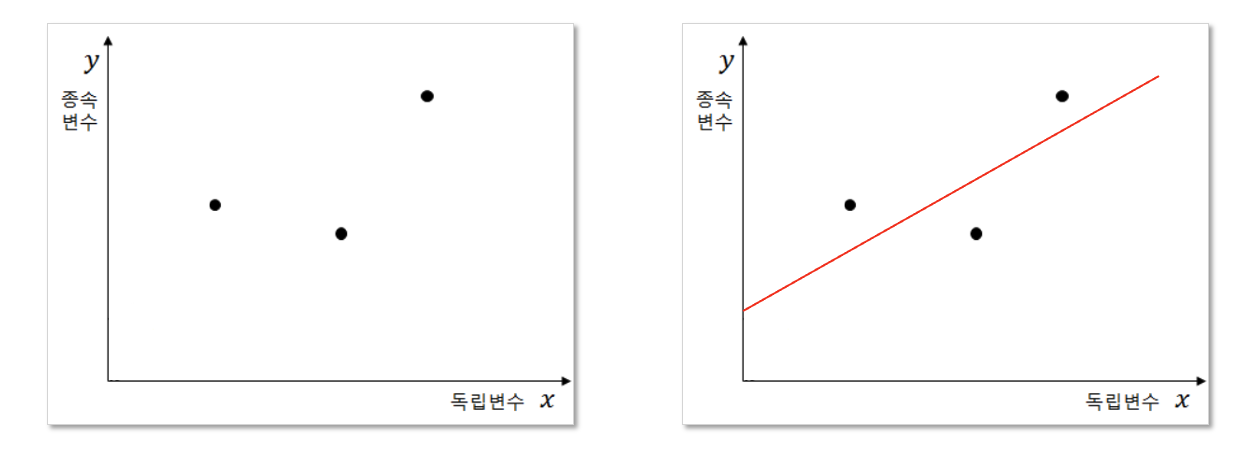
2) Linear Regression
기본적인 선형 회귀 모델인 'y_i=β_0+β_1 x_i+ε_i'에서 'y'는 우리가 예측하고자 하는 종속 변수를 나타내고, 'x'는 그 원인이 되는 독립 변수입니다. 여기서 'β_1'은 기울기를 의미하며, 이는 x의 한 단위 변화가 y에 얼마나 큰 변화를 가져오는지를 나타냅니다. 'β_0'는 y절편으로, x의 값이 0일 때 y의 기댓값을 보여줍니다. 'ε'는 오차항으로, 회귀 모델이 설명하지 못하는 y의 변동성을 나타내며, 이는 독립 변수와 관계없는 무작위 변동을 대표합니다. 선형 회귀 모델은 데이터 포인트들을 가장 잘 대표하는 선을 찾아내어, x와 y 사이의 관계를 직관적으로 이해할 수 있도록 돕습니다. 이러한 모델을 통해 데이터의 기본적인 경향을 파악하고, 변수들 사이의 상호작용을 보다 명확히 파악할 수 있습니다.

3) OLS(Ordinary Least Squares)
OLS(최소제곱법)는 회귀분석에서 가장 기본적이면서도 널리 채택된 방법론입니다. 관측된 데이터 점들에서 직선까지의 수직 거리의 합을 최소화하는 직선을 그리는 방식입니다. 아래 나타난 파란색 선들은 각 데이터 포인트에서 회귀선까지의 잔차를 나타내며, 이 잔차들의 제곱합인 SSE를 최소화함으로써 회귀선을 결정합니다. 이 과정을 통해 추정된 회귀선은 관찰한 데이터를 얼마나 잘 설명하는지를 보여주며, 잔차들을 제곱하여 합산하는 이유는 양의 잔차와 음의 잔차가 상쇄되는 것을 방지하기 위함입니다.

4) BLUE(Best Linear Unbiased Estimator)
선형 회귀분석의 주요 목적을 다시 생각해 보면 설명변수 x와 종속변수 y 사이의 관계를 선형 방정식으로 표현하고자 하는 것입니다. 하지만 현업에서 사용하는 데이터는 이론적 모델보다 훨씬 더 복잡한 형태를 나타내기 때문에, 선형 회귀는 실제 데이터의 패턴을 선형 관계로 단순화하여 근사화하는 데 도움을 줍니다. 이를 위해 데이터가 아래 기본적인 선형 회귀 모델의 가정(BLUE)을 충분히 만족한다고 가정하고, 이를 바탕으로 변수들 간의 상호 작용을 이해하려고 합니다.
- 선형성 : 종속변수와 독립변수 사이에는 선형적인 관계를 띄어야 한다.
- 등분산성 : 잔차의 분산은 독립변수와 무관하게 일정해야 한다.
- 독립성 : 잔차들은 서로 독립적이며, 연관되어 있지 않다.
- 정규성: 잔차가 평균이 0인 정규분포를 띤다.

5) Linear Regression 해석
- E(u| x)가 x값에 의존하지 않으면, 기울기(β_1)는 x가 한 단위 증가할 때, y가 평균 얼마만큼 증가하는지를 나타냅니다.
- 예를 들어, x=교육연수, y=임금일때, 교육연수 1년 차이나는 두 집단 간에는 평균(β_1)만큼의 임금차이가 있습니다.
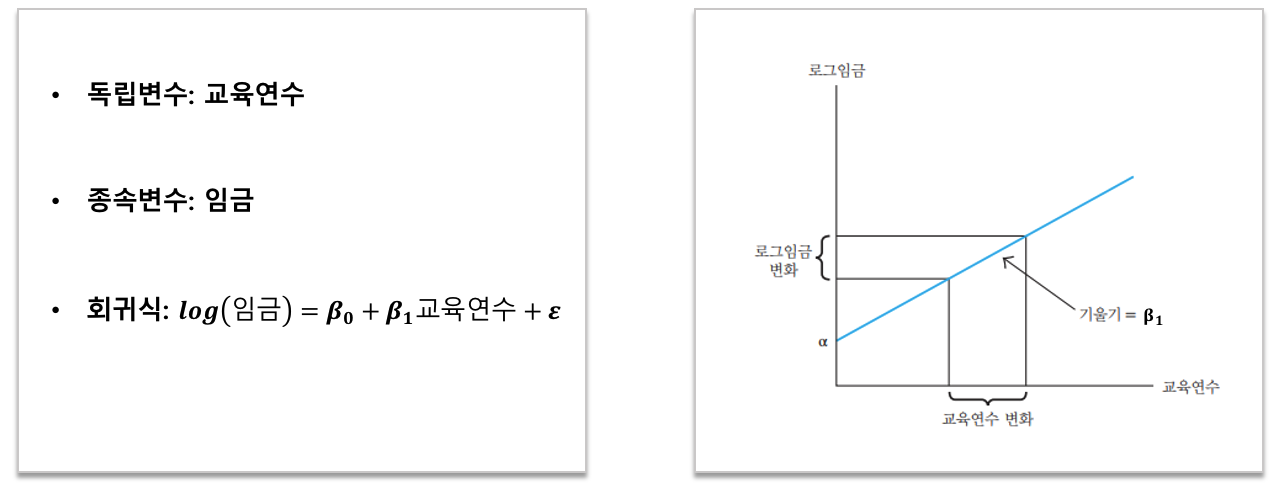
6) Multiple Linear Regression 해석
다중 선형 회귀분석을 논의하기에 앞서, 이번 챕터에서는 모델의 핵심 개념만 간략하게 정리해보려 합니다. 이 모델은 다양한 설명 변수들이 종속 변수에 미치는 영향을 분석하는 데 사용되며, 선형 회귀 방정식을 통해 이러한 관계를 정량화합니다. 일반적인 형태는 y_i = β_0 + β_1x_1 +... + β_kx_k + ε_i로 표현됩니다. 여기서 β_1은 다른 모든 변수(x_2,..., x_k)를 고정한 상태에서 x_1의 변화가 y에 미치는 평균적인 영향을 나타냅니다.

다만, 다중 선형 회귀분석에서 OLS 추정량이 유일하고 신뢰할 수 있기 위해서는 다중공선성이 없어야 한다는 것입니다. 다중 공선성은 독립 변수들 간에 높은 상관관계가 있을 때 발생하며, 이는 추정치의 정확도를 저하시킬 수 있습니다. 이러한 이유로, 모델을 구축하고 해석할 때는 이러한 변수 간의 상호 관계를 신중히 고려해야 합니다. 이제 위 개념들을 바탕으로 모델들의 예시를 살펴보겠습니다.
3. Case Study
1) Simple linear regression (Figure 4.3 ~ 4.4)
스터디 교재의 Figure 4.3에서 제시된 예를 통해 선형 관계의 개념을 살펴보겠습니다. 선형 모델 y = mx + c는 데이터 사이의 관계를 이해하는 데 기본적인 도구로 사용되며, 여기서 m은 기울기를, c는 y절편을 나타냅니다.

위 그래프와 같이 기울기 m이 1.2이고 y절편 c가 5일 때, 선형 방정식은 y = 1.2x + 5로 표현됩니다. 10개의 관측치를 가진 데이터 세트에 이 모델을 적용하면, 각 x값에 대한 y의 예상 값을 계산하여 나타낼 수 있습니다. 그래프에 이러한 점들을 표시하고 연결하면, 관측된 데이터 사이에서 나타나는 일반적인 선형 패턴을 시각적으로 확인할 수 있습니다. 이 방식으로 변수들 사이의 선형 관계를 파악하고, 이해의 폭을 넓힐 수 있습니다.
이어서, 모델의 적합도를 평가하는 과정에 대해 이야기해 보겠습니다. 관측된 데이터와 모델 예측 간의 일치도를 측정하기 위해, SSE를 최소화하는 모델을 찾고자 합니다. 예를 들어, 평균값이 133.7인 10개의 'Final' 값으로 구성된 데이터 세트를 가지고 '임의 모델'을 설정합니다. 이 모델을 기준으로 잔차를 계산하면, 모델의 예측이 실제 관측값에서 얼마나 벗어나는지를 알 수 있습니다.

그림 4.5는 선형 회귀 모델의 잔차를 빨간색 선으로 나타내고 있습니다. 이 선들은 각 관측치가 선형 추세선에서 얼마나 떨어져 있는지를 보여주며, 이러한 거리는 모델이 데이터를 얼마나 잘 예측하는지에 대한 간접적인 지표가 됩니다. 잔차가 작을수록 모델이 관측치를 더 잘 설명하고 있다고 볼 수 있습니다.
한편, 그림 4.6은 관측치들의 Final 값이 평균 133.7 주변에서 어떻게 분포하는지를 보여주고 있습니다. 여기서 '임의 모델'이란 각 관측치의 Final 값에서 전체 평균을 뺀 것을 의미합니다. 이 그림에서 파란색 선들은 각 관측치가 평균으로부터 얼마나 벗어나 있는지, 즉 잔차의 크기를 보여줍니다. 이런 방식으로 잔차를 살펴보면, 데이터가 평균값 주변에 어떻게 분포하는지, 그리고 임의 모델이 실제 데이터의 변동성을 얼마나 포착하는지를 시각적으로 이해할 수 있습니다.

이후 두 개의 선을 합쳐보면 그림 4.7과 같이 모델의 성능을 평가할 수 있습니다. 계산된 결과에서 보듯이, 임의 모델을 사용했을 때의 평균 제곱 잔차는 1574.21인 반면, 회귀 모델을 적용한 후에는 이 값이 398.35로 크게 감소했습니다. 이는 모델이 데이터 변동성의 대략 75%를 설명하고 있다는 것을 의미하며, 결정 계수(R-squared)가 이에 해당하는 변동을 얼마나 잘 예측하는지를 나타냅니다.
2) Case Study - KLIPS 데이터를 활용한 교육 수준과 임금 분석
한국노동연구원이 작성하는 한국노동패널조사로부터 2008년 30~39세 남성 가구주의 교육 수준, 연간 근로소득 등에 대한 자료를 발췌한 것이 Klips데이터에 있습니다. 교육 수준은 educ 변수(단위는 연), 연간 근로소득(세금 공제 후)은 labinc 변수(단위는 백만 원)에) 해당합니다. 교육 수준이 중학교 졸업 이상 (educ=9)인 사람들을 대상으로 하였으며, 박사학위자는 제외하였습니다.
repos <- "http://econ.korea.ac.kr/~chirokhan/local-cran"
install.packages("loedata", repos = repos)
library(loedata)
Klips2 <- subset(Klips, regular==1 & married==1) # 정규직 and 기혼자
summary(Klips2)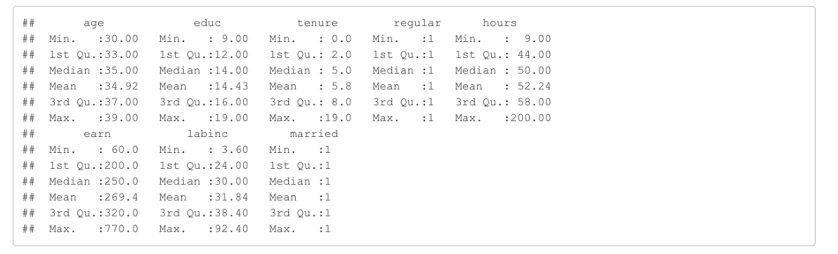
plot(labinc~educ, data=Klips2, log='y')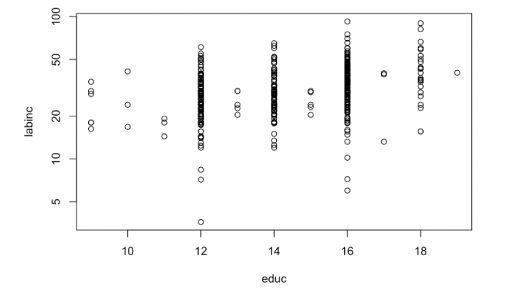
plot(log(labinc)~educ, data=Klips2)
Klips2$mloginc <- with(Klips2, ave(log(labinc), educ, FUN=mean))
points(mloginc~educ, data=Klips2, pch=19, cex=2) # log(labin)의 평균값이 굵은
ggplot(Klips2, aes(x=educ, y=log(labinc)))+
geom_point()+ # 산점도
geom_smooth(method="lm", se=FALSE)+ # 선형 회귀선
theme_minimal() # 깔끔한 테마 적용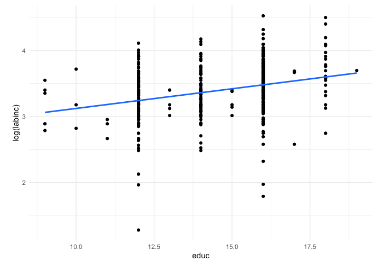
ols <- lm(log(labinc) ~ educ, data=Klips2)
summary(ols)
2) 결론
- 회귀식 : log(labinc)=2.527273+0.059577×educ
- 해석 : 모델의 추정 결과에 따르면, 교육, 수준이 한 단계 올라갈 때마다 연간 근로소득의 로그 변환 값은 평균적으로 약 5.9% 증가하는 것으로 나타났다. 이는 교육이 소득 증가에 긍정적인 영향을 미친다는 명확한 증거를 제시하며, 결과는 통계적으로도 매우 유의미함을 알 수 있다(P < 2e-16).
'People Insight > PA201 스터디' 카테고리의 다른 글
| 다항 로지스틱 회귀분석(Multinomial Logistic Regression)으로 분류 모델 만들어보기 (0) | 2024.02.04 |
|---|---|
| HR 장면에서의 생존분석 (0) | 2024.01.20 |
| [데이터분석 실습] 출퇴근거리에 따른 조기퇴직 확률 분석 (0) | 2023.09.15 |
| 인과효과 추정을 위한 Program Evaluation (0) | 2023.05.28 |
| AI 영상면접기술을 활용한 채용 방식의 타당성 검토 (0) | 2023.05.20 |




